Prefix Conversions (Area and Volume)
Introduction

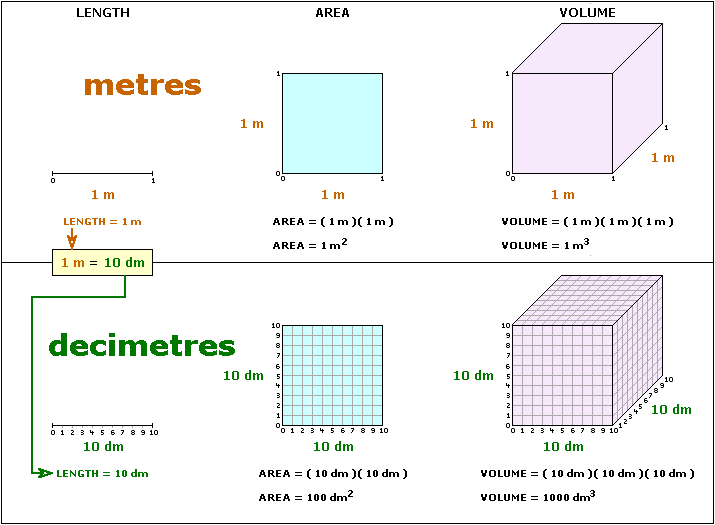
In the illustrations below, the lengths determining the figures all 1 m (or 10 dm since 1 m = 10 dm) .


Chart of Basic Units

Notice that the square in the top illustration has an area of 1 m2, while the equivalent square in the second illustration (with both sides divided into ten equal parts) has an area of 100 dm2.

Notice also that the cube in the top illustration has a volume of 1 m3, while the equivalent cube in the second illustration (with all three sides divided into ten equal parts) has a volume of 1000 dm3.


CONCLUSION: If 1.0 m = 10.0 dm (the decimal is moved one place to the right), then 1.0 m2 = 100.0 dm2 (the decimal is moved two places to the right), and 1.0 m3 = 1000.0 dm3 (the decimal is moved three places to the right).

The Algebra (Length)

Recall the procedure (algebra) to change 3.25 km to centimetres (shown below).


Conversion Example (Length)

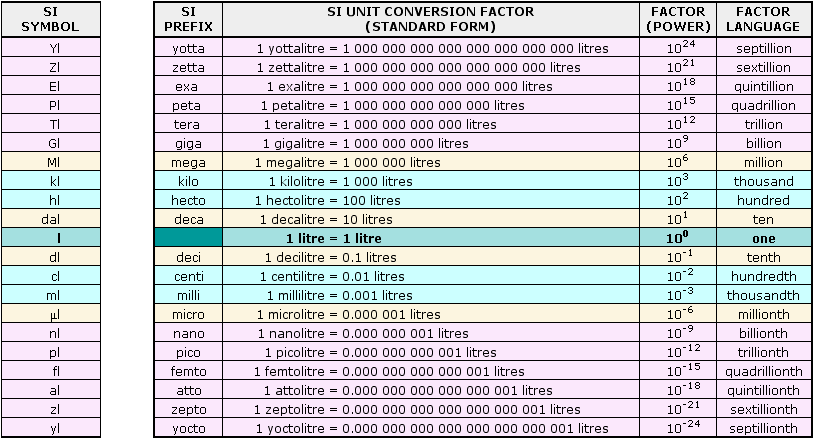
Use the exponents associated with the prefixes of the units you are changing TO and FROM to determine how many places to move the decimal ("kilo" corresponds to a power of ten with an exponent of three, while "centi" corresponds to a power of ten with an exponent of negative two).


3 - (-2) = 5


Move the decimal five places to the right of the original position.

Example of Moving the Decimal (Length)
The Algebra (Area)

The procedure (algebra) to change 3.25 km2 to square centimetres is shown below. Recall that 12 = 1.


Conversion Example (Area)

Use the exponents associated with the prefixes of the units you are changing TO and FROM to determine how many places to move the decimal. Multiply the result by two, since the original units are squared.


2[ 3 - (-2) ] = 2[ 5 ]

2[ 3 - (-2) ] = 10


Move the decimal ten places (or five groups of two) to the right of the original position.

Example of Moving the Decimal (Area)
The Algebra (Volume)

The procedure (algebra) to change 3.25 km3 to cubic centimetres is shown below. Recall that 12 = 1.


Conversion Example (Volume)

Use the exponents associated with the prefixes of the units you are changing TO and FROM to determine how many places to move the decimal. Multiply the result by three, since the original units are cubed.


3[ 3 - (-2) ] = 3[ 5 ]

3[ 3 - (-2) ] = 15


Move the decimal fifteen places (or five groups of three) to the right of the original position.

Example of Moving the Decimal (Volume)
Conversion Applet (Prefixes)
Image only

Instructions text as in global.js

Your browser does not support the canvas element.